In addition to Excel’s 16 standard financial functions, Excel users also have access to another 42 add-in financial functions. Most business users of Excel won’t need these add-in functions, but if you perform much financial analysis with Excel—especially financial analysis of investments—you’ll find frequent occasion to use these tools.
Once you’ve installed the Analysis ToolPak, you can work with the add-in financial functions. You use these functions in the same way that you use other functions, including the financial functions described in the earlier pages of this chapter. The paragraphs that follow describe each of these add-in functions.
Using the Accrued Interest Add-In Functions
Excel provides two functions that help you with accrued interest calculations for securities that pay interest. ACCRINT calculates accrued interest for a security (such as a bond) that pays periodic interest. ACCRINTM calculates accrued interest for a security (such as a zerocoupon bond) that pays interest upon maturity.
The accrued interest functions use a similar set of arguments, including the issue date, first interest date, settlement date, maturity date, coupon rate, par value, frequency, and basis.
The date arguments are self-explanatory for the most part. The issue date is the date the security is issued. The first interest payment date is the first coupon date. The settlement date is the date you purchased, or settled, the bond. The maturity date is the date the bond matures, or expires. You may enter the date arguments either as text strings enclosed in quotation marks (for example, “7/4/99”) or as serial date values (for example, 37000 for April 19, 2001).
The coupon rate and par value arguments let Excel calculate the interest. The coupon rate is the annual interest rate multiplied by the par value to calculate the annual interest. For example, if a bond pays 8% interest annually and the par value is $1,000, Excel would calculate the annual interest by multiplying the 8% by the $1,000 if the coupon is paid annually.
The frequency argument gives the number of coupon payments made each year: you specify 1 to indicate an annual coupon, 2 to indicate a semiannual coupon, and 4 to indicate a quarterly coupon.
The basis argument specifies the number of days in the month and in the year assumed for the date calculations. You specify the basis as 0 for the US (or NASD) version of 30 days in a month and 360 days in a year; as 1 for the actual number of days in the month and year; 2 for the actual number of days in the month but 360 days in a year; 3 for the actual number of days in the month and 365 days in a year; and 4 for the European version of 30 days in a month and 360 days in a year.
Both the ACCRINT and ACCRINTM functions return an error value in the following situations:
- If you enter an invalid date argument, Excel returns #VALUE.
- If the coupon rate or par value argument is less than 0, Excel returns #NUM.
- If the payment frequency is some number other than 1, 2, or 4, Excel returns #NUM.
- If the day-count-basis switch isn’t 1, 2, 3, or 4, Excel returns #NUM.
- If issue date follows the settlement date, Excel returns #NUM.
ACCRINTM
The ACCRINT function calculates the accrued interest for a security that pays periodic interest given the issue date, first interest payment date, settlement date, coupon rate, par value, payment frequency, and a day-count-basis switch. It uses the following syntax:
ACCRINT(issue,first interest,settlement,rate,par,frequency,basis)
For example, if you want to calculate the accrued interest on a bond that was issued on February 8, 1999, first paid interest on April 8, 1999, was purchased on May 23, 2000, pays an 8% coupon, shows a $1,000 par value, pays interest four times a year, and uses the US, or NASD, day-count-basis assumption, you use the following formula:
=ACCRINT(“2/8/99″,”4/8/99″,”5/23/00”,0.08,1000,4,0)
The function returns the value 103.33.
ACCRINTM
The ACCRINTM function calculates the accrued interest for a security that pays interest at maturity given the issue date, the maturity date, coupon rate, par value, and a day-countbasis switch. It uses the following syntax:
ACCRINTM(issue,maturity,rate,par,basis)
For example, if you want to calculate the accrued interest on a bond that was issued on February 8, 1991, matures on May 23, 2010, accrues an 8% coupon, shows a $1,000 par value, accrues interest two times a year, and uses the US, or NASD, day-count-basis assumption, you use the following formula:
=ACCRINTM(“2/8/91″,”5/23/10”,0.08,1000,2)
The function returns the value 1565.33.
Using the Bond Duration Add-In Functions
Excel provides two functions that let you make bond duration calculations: DURATION and MDURATION. Duration, a weighted average measure of the present value of a bond’s cash flows, quantifies how a change in the bond yield affects the bond price.
Both duration functions use the same set of six arguments: the settlement date, the maturity date, the coupon rate, the yield, the coupon frequency, and the day count basis.
The settlement date specifies the date the bond is settled, or purchased. The maturity date specifies the date the bond matures, or expires. As with the other add-in financial functions, you may enter the date arguments either as text strings enclosed in quotation marks or as serial date values.
The coupon rate argument is the bond’s interest rate and is used to calculate coupon payments. The yield argument is the bond’s annual yield.
The frequency argument gives the number of coupon payments made each year: you specify 1 to indicate an annual coupon, 2 to indicate a semiannual coupon, and 4 to indicate a quarterly coupon.
The basis argument specifies the number of days in the month and year assumed for the date calculations. You specify the basis as 0 for the US (or NASD) version of 30 days in a month and 360 days in a year; as 1 for the actual number of days in the month and actual number of days; 2 for the actual number of days in the month but 360 days in a year; 3 for the actual number of days in the month and 365 days in a year; and 4 for the European version of 30 days in a month and 360 days in a year.
The duration functions return an error value in several predictable cases:
- If you use an invalid date, Excel returns #VALUE. Note that this means your date arguments must make sense collectively, too. For example, your maturity date must follow the settlement date.
- If you use a frequency argument other than 1, 2, or 4, Excel returns #NUM.
- If you use a day-count-basis switch other than 0, 1, 2, 3, or 4, Excel returns #NUM
- If the settlement day follows the maturity date, Excel returns #NUM
- If the rate or yield is less than zero, Excel returns #NUM
DURATION
The DURATION function calculates a Macauley duration given the settlement date, maturity date, coupon rate, yield, frequency, and basis. It uses the following syntax:
DURATION(settlement,maturity,coupon,yield,frequency,basis)
For example, suppose you want to calculate the duration of a bond you purchased on April 23, 2000, and that will mature on November 30, 2020. Further suppose that the coupon rate is 8%, which is paid in four quarterly payments, but that the bond yield is 7%. If you want to use the US (NASD) day count basis of 30 days in a month and 360 days in a year, you would use the following formula to calculate this bond’s yield:
=DURATION(“4/23/2000″,”11/30/2020”,.08,.07,4,0)
The formula returns the value 10.6496.
MDURATION
The MDURATION function calculates a modified duration given the settlement date, maturity date, coupon rate, yield, frequency, and basis. It uses the following syntax:
MDURATION(settlement,maturity,coupon,yield,frequency,basis)
For example, suppose you want to calculate the duration of a bond you purchased on April 23, 2000, and that will mature on November 30, 2020. Further suppose that the coupon rate is 8%, which is paid in four quarterly payments, but that the bond yield is 7%. If you want to use the US (NASD) day count basis of 30 days in a month and 360 days in a year, you would use the following formula to calculate this bond’s yield:
=MDURATION(“4/23/2000″,”11/30/2020”,.08,.07,4,0)
The formula returns the value 10.4664.
Using the Capital Budgeting Add-In Functions
Excel provides standard functions, IRR and NPV, for calculating the internal rate of return and net present value of a set of cash flows. While most often you’ll want to use these two functions, they may sometimes present a practical problem: Both the IRR and NPV functions assume you’ve first constructed a worksheet that arranges the cash flows into equal periods. In other words, to use the IRR or NPV function, you must first construct a worksheet that shows the investment’s monthly cash flows, or its annual cash flows, or the cash flows from some other consistent time period.
Unlike the IRR and the NPV functions, the XIRR and XNPV functions don’t require you to first construct a worksheet schedule that arranges the investment cash flows into equal periods. With the XIRR and XNPV functions, you supply the date values that correspond to the cash flow values to the function as arguments.
The somewhat unique feature of both the XIRR and the XNPV function is that if you supply the actual date values or cash flow values inside the formula as arguments, they expect you to supply the values argument and the dates argument as arrays. (An array is just a set of numbers.)
For example, suppose that you want to calculate the internal rate of return and net present value for an investment that produces the following cash flows on the following dates:
1/1/2000 -1000
12/31/2000 -1000
4/15/2001 2000
12/31/2001 1000
If you include the actual array in the argument, you can designate the array by enclosing the values and dates arguments inside braces. To show the preceding date values in an array, for example, you would type the following:
{“1/1/2000″,”12/31/2000″,”4/15/2001″,”12/31/2001”}
To show the preceding cash flow values as an array, you would type the following:
{-1000,-1000,2000,1000}
If you enter the date values and cash flow values in worksheet ranges, you don’t need to worry about identifying the date values and cash flow values as arrays. For example, if you enter the preceding set of date values in the worksheet range A1:A4 and the preceding set of cash flow values in the worksheet range B1:B4, you can use these worksheet ranges as the function arguments.
The XIRR and XNPV functions, predictably, require you to use date values that are valid. You must also use the same number of date values as you use cash flow values. If you supply an invalid argument or set of arguments, Excel returns the #NUM error value.
XIRR
The XIRR function calculates the internal rate of return for an investment given its cash flows, the dates of those cash flows, and, optionally, an initial guess as to the internal rate of return. The function uses the following syntax:
XIRR(values,dates,guess)
For example, suppose that you want to calculate the internal rate of return for an investment that produces the following cash flows on the following dates:
1/1/2000 -1000
12/31/2000 -1000
4/15/2001 2000
12/31/2001 1000
To calculate the internal rate of return for this set of cash flows using the XIRR function and using a starting guess of 20%, you would use the following formula:
=XIRR({-1000,-1000,2000,1000},{“1/1/2000″,”12/31/2000″,”4/15/2001″,”12/ 31/2001”},.2)
The formula returns the value .470251, which is equivalent to 47.0251% annually.
If the date values were stored in the worksheet range A1:A4 and the cash flow values were stored in the worksheet range B1:B4, you could instead use the following formula:
=XIRR(B1:B4,A1:A4,.2)
XNPV
The XNPV function calculates the net present value for an investment given its cash flows, the dates of those cash flows, and the annual discount rate. The function uses the following syntax:
XNPV(rate,values,dates)
For example, suppose that you want to calculate the net present value for an investment that produces the following cash flows on the following dates:
1/1/2000 -1000
12/31/2000 -1000
4/15/2001 2000
12/31/2001 1000
If the date values were stored in the worksheet range A1:A4, the cash flow values were stored in the worksheet range B1:B4, and you wanted to use a discount rate of 15%, you would use the following formula:
=XNPV(.15,B1:B4,A1:A4)
The formula returns the value 557.17.
Curiously, the XNPV function doesn’t accept date values supplied as text strings. For example, although the following formula is equivalent to the preceding one, it returns the #VALUE error value:
=XNPV(.15,{-1000,-1000,2000,1000},{“1/1/2000″,”12/31/2000″,”4/15/ 2001″,”12/31/2001”})
You could, however, rewrite this formula using equivalent serial date values (the serial date 36526 for 1/1/2000, the serial date value 36891 for 12/31/2000, and so on), and then Excel returns the correct net present value:
=XNPV(0.15,{-1000,-1000,2000,1000},{36526,36891,36996,37256})
Using the Coupon Dates Add-In Functions
Excel provides six functions that let you make coupon date calculations more easily: COUPDAYBS, COUPDAYS, COUPDAYSNC, COUPNCD, COUPNUM, and COUPPCD.
All six coupon date functions use four standard arguments: the settlement date, the maturity date, the frequency, and the basis.
The settlement date specifies the date the bond is settled, or purchased. The maturity date specifies the date the bond matures, or expires. You may enter these date arguments either as text strings enclosed in quotation marks or as serial date values.
The frequency argument gives the number of coupon payments made each year: you specify 1 to indicate an annual coupon, 2 to indicate a semiannual coupon, and 4 to indicate a quarterly coupon.
sThe basis argument specifies the number of days in the month and year assumed for the date calculations. You specify the basis as 0 for the US (or NASD) version of 30 days in a month and 360 days in a year; as 1 for the actual number of days in the month and actual number of days; 2 for the actual number of days in the month but 360 days in a year; 3 for the actual number of days in the month and 365 days in a year; and 4 for the European version of 30 days in a month and 360 days in a year.
The coupon date functions return an error value in several predictable cases:
- If you use an invalid date, Excel returns #VALUE
- If you use a frequency argument other than 1, 2, or 4, Excel returns #NUM
- If you use a day-count-basis switch other than 0, 1, 2, 3, or 4, Excel returns #NUM
- If the settlement day follows the maturity date, Excel returns #NUM
COUPDAYBS
The COUPDAYBS function calculates the number of days from the last coupon payment date to the settlement date given the settlement date, maturity date, coupon frequency, and basis. It uses the following syntax:
COUPDAYBS(settlement,maturity,frequency,basis)
For example, suppose you want to calculate the number of days from the last coupon payment date to the settlement date in the following situation: Someone purchases a 10-year bond on November 26, 2000, with a maturity date of April 30, 2008. The bond pays coupons twice a year based on the US, or NASD, assumption. To make this calculation, you use the following formula:
COUPDAYBS(“11/26/2000″,”4/30/2008”,2,0)
The function returns the value 26.
COUPDAYS
The COUPDAYS function calculates the number of days in the coupon period that includes the settlement date given the settlement date, the maturity date, the coupon frequency, and the day count basis. It uses the following syntax:
COUPDAYS(settlement,maturity,frequency,basis)
For example, suppose you want to calculate the number of days in the coupon payment in the following situation: Someone purchases a 10-year bond on November 26, 2000, with a maturity date of April 30, 2008. The bond pays its coupon twice a year based on the US, or NASD, assumption. To make this calculation, you use the following formula:
=COUPDAYS(“11/26/2000″,”4/30/2008”,2,0)
The function returns the value 180.
COUPDAYBS
The COUPDAYBS function calculates the number of days from the last coupon payment date to the settlement date given the settlement date, maturity date, coupon frequency, and basis. It uses the following syntax:
COUPDAYBS(settlement,maturity,frequency,basis)
For example, suppose you want to calculate the number of days from the last coupon payment date to the settlement date in the following situation: Someone purchases a 10-year bond on November 26, 2000, with a maturity date of April 30, 2008. The bond pays coupons twice a year based on the US, or NASD, assumption. To make this calculation, you use the following formula:
COUPDAYBS(“11/26/2000″,”4/30/2008”,2,0)
The function returns the value 26.
COUPDAYSNC
The COUPDAYSNC function calculates the number of days from the settlement date to the next coupon date given the settlement date, the maturity date, the frequency, and the basis. It uses the following syntax:
COUPDAYSNC(settlement,maturity,frequency,basis)
For example, suppose you want to calculate the number of days from the settlement date to the next coupon payment in the following situation: Someone purchases a 10-year bond on November 26, 2000, with a maturity date of April 30, 2008. The bond pays its coupon twice a year based on the US, or NASD, assumption. To make this calculation, you use the following formula:
=COUPDAYSNC(“11/26/2000″,”4/30/2008”,2,0)
The function returns the value 154.
COUPNCD
The COUPNCD function calculates the coupon date that follows the settlement date given the settlement date, the maturity date, the frequency, and the day-count-basis switch. It uses the following syntax:
COUPNCD(settlement,maturity,frequency,basis)
For example, suppose you want to calculate the next coupon payment after the settlement date in the following situation: Someone purchases a 10-year bond on November 26, 2000, with a maturity date of April 30, 2008. The bond pays its coupon twice a year based on the US, or NASD, assumption. To make this calculation, you use the following formula:
=COUPNCD(“11/26/2000″,”4/30/2008”,2,0)
The function returns the value 37011, which is the serial date value for April 30, 2001.
COUPNUM
The COUPNUM function calculates the number of number of coupons, or interest payments, made between the settlement date and maturity date. The function, which rounds this result up to the nearest integer value, uses the following syntax:
COUPNUM(settlement,maturity,frequency,basis)
For example, suppose you want to calculate the number of coupons, or interest payments, in the following situation: Someone purchases a 10-year bond on November 26, 2000, with a maturity date of April 30, 2008. The bond pays its coupon twice a year based on the US, or NASD, assumption. To make this calculation, you use the following formula:
=COUPNUM(“11/26/2000″,”4/30/2008”,2,0)
The function returns the value 15.
COUPPCD
The COUPPCD function calculates the coupon date before the settlement date given the settlement date, the maturity date, the frequency, and the basis. It uses the following syntax:
COUPPCD(settlement,maturity,frequency,basis)
For example, suppose you want to calculate the coupon payment date preceding the settlement date in the following situation: Someone purchases a 10-year bond on November 26, 2000, with a maturity date of April 30, 2008. The bond pays its coupon twice a year based on the US, or NASD, assumption. To make this calculation, you use the following formula:
COUPPCD(“11/26/2000″,”4/30/2008”,2,0)
The function returns the value 36830, which is the serial date value for October 31, 2000.
Using the Cumulative Interest and Principal Add-In Functions
Excel supplies two functions specifically for calculating cumulative interest and principal payments on a loan: CUMIPMT, which calculates the cumulative interest payments on a bond or note, and CUMPRINC, which calculates the cumulate principal payments on a bond or note.
Both functions use the same set of arguments, including the interest rate, the loan term (or number of periods), the loan balance (or present value), the starting date and the ending date of the period for which you want to calculate the cumulative interest or principal payments, and a type-of-annuity switch to indicate whether the stream of payments occurs as an ordinary annuity or an annuity due.
The interest rate, loan term, loan balance, and type-of-annuity switch arguments work the same way for the CUMIPMT and CUMPRINC functions as they work for the standard financial functions.
The starting date and ending date arguments, as noted earlier, simply provide the starting and ending points for the period of time for which you want to calculate the cumulative interest or principal paid.
Both the CUMIPMT and CUMPRINC functions return an error value in several predictable situations as well as one surprising situation:
- If the interest rate or the loan term rate is less than or equal to zero.
- If the starting date or ending date is nonsensical or if the starting date follows the ending date.
- If the loan present value is less than or equal to zero. (Note that this means you don’t use the convention of specifying the loan present value as a negative number to show that it’s a cash outflow.)
CUMIPMT
The CUMIPMT function calculates the cumulative interest paid on a loan between two dates you specify given the interest rate, loan term, loan present value, the starting date and ending date, and the type-of-annuity switch. It uses the following syntax:
CUMIPMT(rate,nper,pv,start period,end period,type)
Suppose, for example, that you want to calculate the cumulative interest paid on a $1,000,000, ten-year equipment loan that charges 9% interest and requires monthly payments arranged as an annuity due. Further suppose that you want to calculate the cumulative interest payments made over the first five years, or sixty months. To make this calculation, you use the following formula:
=CUMIPMT(.09/12,10*12,1000000,1,60,1)
The function returns the value –360094.
CUMPRINC
The CUMPRINC function calculates the cumulative principal paid on a loan between two dates you specify given the interest rate, loan term, loan present value, the starting date and ending date, and the type-of-annuity switch. It uses the following syntax:
CUMPRINC(rate,nper,pv,start period,end period,type)
Suppose, for example, that you want to calculate the cumulative principal paid on a $1,000,000, ten-year equipment loan that charges 9% interest and requires monthly payments arranged as an annuity due. Further suppose that you want to calculate the cumulative principal payments made over the first five years, or sixty months. To make this calculation, you use the following formula:
=CUMPRINC(.09/12,10*12,1000000,1,60,1)
The function returns the value –394303.
Using the Dollar Pricing Add-In Functions
Excel’s DOLLARDE and DOLLARFR functions let you easily convert security dollar prices from decimal prices to fractional prices or from fractional prices to decimal prices.
DOLLARDE
The DOLLARDE function, for example, converts a fractional dollar price to an equivalent decimal price based on the fractional price and the fraction’s denominator. It uses the following syntax:
DOLLARDE(fractional price,fraction)
For example, to convert the fractional price 25 2/16 to an equivalent decimal price, you use the following formula:
=DOLLARDE(25.02,16)
The function returns the value 25.125.
And to convert the fractional price 25 1/8 to an equivalent decimal price, you use the following formula:
=DOLLARDE(25.1,8)
This function returns the value 25.125.
DOLLARFR
The DOLLARFR functions converts a dollar decimal price into a dollar fractional price given the decimal price and the fraction’s denominator. It uses the following syntax:
DOLLARFR(decimal price,fraction)
For example, to convert the price 10.125 to a fractional price in eighths, you use the following formula:
=DOLLARFR(10.125,8)
The function returns the value 10.1.
Similarly, to convert the price 10.125 to a fractional price in sixteenths, you use the following formula:
=DOLLARFR(10.125,16)
The function returns the value 10.02.
Using the French Depreciation Add-In Functions
Excel supplies two special functions for making French depreciation calculations, AMORDEGRC and AMORLINC. Both functions use a similar sets of arguments, including the asset cost, purchase date, date at the end of the first period, salvage value, accounting period, depreciation rate, and basis. You specify the basis as 0 for the US (or NASD) version of 30 days in a month and 360 days in a year; as 1 for the actual number of days in the month and year; 2 for the actual number of days in the month but 360 days in a year; 3 for the actual number of days in the month and 365 days in a year; and 4 for the European version of 30 days in a month and 360 days in a year.
AMORDEGRC
The AMORDEGRC function uses the following syntax:
AMORDEGRC(cost,purchase date,first period,salvage,period,rate,basis)
For example, if you want to depreciate a piece of equipment purchased on July 15, 2000, for 3,000 French francs, using a salvage value of 600 French francs, a 15% depreciation rate, and the first accounting period ends on December 31, 2000, you use the following formula:
=AMORDEGRC(3000,”7/15/2000″,”12/31/2000″,600,1,0.15,1)
The AMORDEGRC function returns the value 930.
- The function uses different coefficients depending on the asset’s estimated life. If the life of the asset falls between three and four years, the function uses a depreciation coefficient equal to 1.5. If the life of the asset falls between five and six years, the function uses a depreciation coefficient equal to 2. If the life of the asset is greater than six years, the function uses a depreciation coefficient equal to 2.5.
- To fully depreciate an asset, the depreciation rate grows to 50% for the next-to-last period and 100% for the last period.
- If you specify the estimated economic life of an asset as a non-integer value between 0 and 5—such as 4.5 for example—the AMORDEGRC function returns the #NUM! error value.
AMORLINC
The AMORLINC function uses the following syntax:
AMORLINC(cost,purchase date,first period,salvage,period,rate,basis)
For example, if you want to depreciate a piece of equipment purchased on July 15, 2000, for 3,000 French francs, using a salvage value of 600 French francs, a 15% depreciation rate, and the first accounting period ends on December 31, 2000, you use the following formula:
=AMORLINC(3000,”7/15/2000″,”12/31/2000″,600,1,0.15,1)
The function returns the value 450.
Using the Future Value Add-In Functions
Two of the add-in functions don’t really fit into one of the other categories, but because they both calculate the future value of some investment, I’ve grouped them together as future value functions: FVSCHEDULE and RECEIVED.
FVSCHEDULE
The FVSCHEDULE function calculates the future value of an investment given the present value of the investment and a schedule of interest rates. The function uses the following syntax:
FVSCHEDULE(principal,rate schedule)
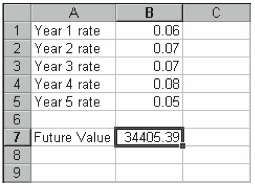
As an example of how this function works, suppose you want to calculate the future value of an initial investment equal to $25,000 invested over the next five years at the following annual interest rates: .06, .07, .07, .08, .05. The following formula makes this calculation:
=FVSCHEDULE(25000,{.06,.07,.07,.08,.05})
If the annual interest rates are stored in the worksheet range B1:B5, as shown in Figure 5-7, you might also use the following formula:
=FVSCHEDULE(25000,B1:B5)
Both functions return the same value, 34405.39.
RECEIVEDM
The RECEIVED function calculates the future value amount of a fully invested, or zerocoupon, security given its settlement date, maturity date, the initial investment, the discount rate, and the basis. The function uses the following syntax:
RECEIVED(settlement,maturity,investment,discount,basis)
The settlement date specifies the date the bond is settled, or purchased. The maturity date specifies the date the bond matures, or expires. You may enter these date arguments either as text strings enclosed in quotation marks or as serial date values.
The investment is the initial amount invested, or the present value.
The discount rate specifies the annual discount rate used to price the bill.
Finally, the familiar basis argument specifies the number of days in the month and in the year assumed for the date calculations. You specify the basis as 0 for the US (or NASD) version of 30 days in a month and 360 days in a year; as 1 for the actual number of days in the month and year; 2 for the actual number of days in the month but 360 days in a year; 3 for the actual number of days in the month and 365 days in a year; and 4 for the European version of 30 days in a month and 360 days in a year.
For example, suppose you want to calculate the future value amount received for a bond you purchase on May 1, 2000, and that matures on October 31, 2002. Further suppose that you purchased the bond for $50,000 based on a 6% discount rate. If you want to use the US (or NASD) day-count-basis assumption, you use the following formula:
=RECEIVED(“5/1/2000″,”10/31/2002”,50000,.06,0)
The function returns the value 58823.53.
Using the Interest Rate Add-In Functions
Excel provides four functions that let you make interest rate calculations: DISC, EFFECT, INTRATE, and NOMINAL.
The DISC and INTRATE functions, which are related, work from the same basic set of arguments: the settlement date, the maturity date, the redemption value, the price, the frequency, and the basis.
The settlement date specifies the date the bond is settled, or purchased. The maturity date specifies the date the bond matures, or expires. You may enter the date arguments either as text strings enclosed in quotation marks (for example, “7/4/99”) or as serial date values (for example, 37000 for April 19, 2001.)
The redemption argument is the bond’s redemption value per each $100 of face value.
The price argument shows the price of a bond expressed as a percentage of its face value. For example, a bond that cost $991.83 would be priced at 99.183.
The frequency argument gives the number of coupon payments made each year: you specify 1 to indicate an annual coupon, 2 to indicate a semiannual coupon, and 4 to indicate a quarterly coupon.
The basis argument specifies the number of days in the month and in the year assumed for the date calculations. You specify the basis as 0 for the US (or NASD) version of 30 days in a month and 360 days in a year; as 1 for the actual number of days in the month and year; 2 for the actual number of days in the month but 360 days in a year; 3 for the actual number of days in the month and 365 days in a year; and 4 for the European version of 30 days in a month and 360 days in a year.
The EFFECTIVE and NOMINAL functions, which are also related, work from a set of three arguments: the effective annual interest rate, the nominal interest rate, and the number of compounding periods in the year.
DISC
The DISC function calculates the discount rate for a security—the amount by which the redemption value is reduced expressed as an annual percentage—given its settlement date, maturity date, price, redemption, and basis. The function uses the following syntax:
DISC(settlement,maturity,price,redemption,basis)
For example, suppose you want to calculate the discount rate on a zero-coupon, $100 redemption-value bond that you purchased on July 10, 2000, for 99.875. If you choose to use the US (or NASD) day-count-basis assumption, you use the following formula to make this calculation:
=DISC(“7/10/2000″,”11/30/2000”,97.875,100,0)
The function returns the value .054643, which is equivalent to 5.4643%.
EFFECT
The EFFECT function calculates the effective annual interest given the stated annual interest rate and the number of annual compounding periods. The function uses the following syntax:
EFFECT(nominal rate,compounding periods)
For example, if you want to calculate the effective interest rate when the nominal rate is 6%, but this rate is compounded daily (based on a 360-day year), you use the following formula:
=EFFECT(.06,360)
The function returns the value .061831, which is equivalent to 6.1831%.
INTRATE
The INTRATE function calculates the interest rate for a fully invested, or zero-coupon, security given its settlement date, maturity date, the initial investment amount, the redemption value, and the basis. The function uses the following syntax:
INTRATE(settlement,maturity,investment,redemption,basis)
For example, suppose you want to calculate the interest rate on a zero-coupon, $100 redemption-value bond that you purchased on July 10, 2000, for 99.875. If you choose to use the US (or NASD) day-count basis assumption, you use the following formula to make this calculation:
=INTRATE(“7/10/2000″,”11/30/2000”,97.875,100,0)
The function returns the value .055829, which is equivalent to 5.5829%.
NOMINAL
The function calculates the nominal annual interest given the effective annual interest rate and the number of annual compounding periods. The function uses the following syntax:
NOMINAL(effective rate,compounding periods)
For example, if you want to calculate the nominal interest rate when the effective rate is 6.1831% and this rate is based on daily compounding (based on a 360-day year), you use the following formula:
=NOMINAL(.061831,360)
The function returns the value .06, which is equivalent to 6%.
Using the Price and Yield Add-In Functions
Excel provides 10 functions that let you make discount, yield, and price calculations for securities such as bonds more easily: ODDFPRICE, ODDFYIELD, ODDLPRICE, ODDLYIELD, PRICE, PRICEDISC, PRICEMAT, YIELD, YIELDDISC, and YIELDMAT.
As a group, the 10 yield and price functions use a set of standard arguments: the settlement date, the maturity date, the frequency, and the basis.
The yield and price functions use several standard date arguments, for example. The settlement date specifies the date the bond is settled, or purchased. The maturity date specifies the date the bond matures, or expires. The issue date is the date on which a security is issued. You may enter the date arguments either as text strings enclosed in quotation marks (for example, “7/4/99”) or as serial date values (for example, 37000 for April 19, 2001.)
The functions for pricing odd-period securities—ODDFPRICE, ODDFYIELD, ODDLPRICE, and ODDLYIELD—also require the date of the first regular coupon payment or the date of the last regular coupon payment in order to calculate the first or last odd period.
The rate argument is the bond’s interest rate. The yield argument is the bond’s annual yield. The redemption argument is the bond’s redemption value per each $100 of face value.
The price argument shows the price of a bond expressed as a percentage of its face value. For example, a bond that cost $991.83 would be priced at 99.183.
The frequency argument gives the number of coupon payments made each year: you specify 1 to indicate an annual coupon, 2 to indicate a semiannual coupon, and 4 to indicate a quarterly coupon.
The basis argument specifies the number of days in the month and year assumed for the date calculations. You specify the basis as 0 for the US (or NASD) version of 30 days in a month and 360 days in a year; as 1 for the actual number of days in the month and year; 2 for the actual number of days in the month but 360 days in a year; 3 for the actual number of days in the month and 365 days in a year; and 4 for the European version of 30 days in a month and 360 days in a year.
The yield and price functions return the #NUM error value in several predictable cases:
- If you use an invalid date, Excel returns #VALUE. Note that this means your date arguments must make sense collectively, too. For example, your maturity date must follow the settlement date.
- If you use a frequency argument other than 1, 2, or 4, Excel returns #NUM.
- If you use a day-count-basis switch other than 0, 1, 2, 3, or 4, Excel returns #NUM.
- If the rate or yield or price is less than zero, Excel returns #NUM.
ODDFPRICE
The ODDFPRICE function calculates the price per $100 face value of a security when the first period is odd—shorter or longer than a typical coupon period—given the settlement date, maturity date, issue date, first coupon date, coupon rate, yield, redemption price, coupon frequency, and basis. It uses the following syntax:
ODDFPRICE(settlement,maturity,issue,first coupon,rate,yield,redemption,frequency,basis)
Suppose, for example, that you want to calculate the price of an odd-period bond that you purchased on March 4, 2000, that will mature on May 31, 2011, was originally issued on December 7, 1999, pays a semiannual coupon of 3.5% starting on November 30, 2000, and is priced to yield 6.5% annually. Further assume that you want to use the European, 30-daysin-a-month, 360-days-in-a-year day count basis. To make this calculation, you use the following formula:
=ODDFPRICE(“3/4/2000″,”5/31/2011″,”12/7/1999″,”11/30 2000”, .035*2,.065,100,2,4)
The function returns 100.5063.
ODDFYIELD
The ODDFYIELD function calculates the yield of a security when the first period is odd— shorter or longer than a typical coupon period—given the settlement date, maturity date, issue date, first coupon date, coupon rate, price, redemption price, coupon frequency, and basis. It uses the following syntax:
ODDFYIELD(settlement,maturity,issue,first coupon,rate,price,redemption, frequency,basis)
Suppose, for example, that you want to calculate the price on an odd-period bond that you purchased on March 4, 2000, that will mature on May 31, 2011, was originally issued on December 7, 1999, pays a semiannual coupon of 3.5% starting on November 30, 2000, and is priced at 99.183 but will be redeemed at face value. Further assume that you want to use the European, 30-days-in-a-month, 360-days-in-a-year day count basis. To make this calculation, you use the following formula:
=ODDFYIELD(“3/4/2000″,”5/31/2011″,”12/7/1999″,”11/30/2000”, .035*2,99.183,100,2,4)
The function returns 0.066599, which is equivalent to 6.6599%.
ODDLPRICE
The ODDLPRICE function calculates the price per $100 face value of a security when the last period is odd—shorter or longer than a typical coupon period—given the settlement date, maturity date, issue date, last coupon date, coupon rate, yield, redemption price, coupon frequency, and basis. It uses the following syntax:
ODDLPRICE(settlement,maturity,last coupon,rate,yield,redemption,frequency,basis)
Suppose, for example, that you want to calculate the price on an odd-period bond that you purchased on March 4, 2000, that will mature on May 31, 2011, was originally issued on December 7, 1998, pays a semiannual coupon of 3.5%, last paid interest on November 30, 1999, and is priced to yield 6.5% annually. Further assume that you want to use the European, 30-days-in-a-month, 360-days-in-a-year day count basis. To make this calculation, you use the following formula:
=ODDLPRICE(“3/4/2000″,”5/31/2011″,”11/30/1999”,.035*2,.065,100,2,4)
The function returns 102.4757.
ODDLYIELD
The ODDFYIELD function calculates the yield of a security when the last period is odd— shorter or longer than a typical coupon period—given the settlement date, maturity date, issue date, last coupon date, coupon rate, price, redemption price, coupon frequency, and basis. It uses the following syntax:
ODDLYIELD(settlement,maturity,issue,last coupon,rate,price,redemption, frequency,basis)
Suppose, for example, that you want to calculate the price on an odd-period bond that you purchased on March 4, 2000, that will mature on May 31, 2011, was originally issued on December 7, 1999, pays a semiannual coupon of 3.5%, last paid a coupon on November 30, 1999, and is priced at 99.183 but will be redeemed at face value. Further assume that you want to use the European, 30-days-in-a-month, 360-days-in-a-year day count basis. To make this calculation, you use the following formula:
=ODDLYIELD(“3/4/2000″,”5/31/2011″,”11/30/1999”,.035*2,99.183,100,2,4)
The function returns 0.070019, which is equivalent to 7.0019%.
PRICE
The PRICE function calculates the price per $100 face value of a security given the settlement date, maturity date, coupon rate, yield, redemption price, coupon frequency, and basis. It uses the following syntax:
PRICE(settlement,maturity,rate,yield,redemption,frequency,basis)
Suppose, for example, that you want to calculate the price on a bond that you purchased on March 4, 2000, that will mature on May 31, 2011, pays a semiannual coupon of 3.5%, is priced to yield 6.5% annually, and will be redeemed at face value, or 100. Further assume that you want to use the European, 30-days-in-a-month, 360-days-in-a-year day count basis. To make this calculation, you use the following formula:
=PRICE(“3/4/2000″,”5/31/2011”,.035*2,.065,100,2,4)
The function returns 103.9299.
PRICEDISC
The PRICEDISC function calculates the price per $100 face value of a discounted security given the settlement date, maturity date, discount rate, redemption price, and basis. It uses the following syntax:
PRICEDISC(settlement,maturity,discount,redemption,basis)
Suppose, for example, that you want to calculate the price on a discounted security that you purchased on March 4, 2000, that will mature on May 31, 2011, is discounted using a rate of 6.5% annually, and will be redeemed at face value, or 100. Further assume that you want tousetheEuropean,30-days-in-a-month,360-days-in-a-yeardaycountbasis.Tomakethis calculation, you use the following formula:
=PRICEDISC(“3/4/2000″,”5/31/2011”,.065,100,4)
The function returns 26.9472.
PRICEMAT
The PRICEMAT function calculates the price per $100 face value of a security that will pay its interest upon maturity given the settlement date, maturity date, issue date, coupon rate, yield, and basis. It uses the following syntax:
PRICEMAT(settlement,maturity,issue,rate,yield,basis)
Suppose, for example, that you want to calculate the price on a security that you purchased on March 4, 2000, was first issued on March 4, 1999, that will mature on May 31, 2011, pays a coupon of 3.5% semiannually, and is discounted using a rate of 6.5% annually. Further assume that you want to use the European, 30-days-in-a-month, 360-days-in-a-year day count basis. To make this calculation, you use the following formula:
=PRICEMAT(“3/4/2000″,”5/31/2011″,”3/4/1999”,.035*2,.065,4)
The function returns 100.2923.
YIELD
The YIELD function calculates the yield of a security given the settlement date, maturity date, coupon rate, price, redemption price, coupon frequency, and basis. It uses the following syntax:
YIELD(settlement,maturity,rate,price,redemption,frequency,basis)
Suppose, for example, that you want to calculate the yield on a bond that you purchased on March 4, 2000, that will mature on May 31, 2011, pays a semiannual coupon of 3.5%, is priced at 101.1425, and will be redeemed at face value, or 100. Further assume that you want tousetheEuropean,30-days-in-a-month,360-days-in-a-yeardaycountbasis.Tomakethis calculation, you use the following formula:
=YIELD(“3/4/2000″,”5/31/2011”,.035*2,101.1425,100,2,4)
The function returns 0.068507, which is equivalent to 6.8507%.
YIELDDISC
The YIELDDISC function calculates the yield of a discounted security given the settlement date, maturity date, price, redemption price, and basis. It uses the following syntax:
YIELDDISC(settlement,maturity,price,redemption,basis)
Suppose, for example, that you want to calculate the yield on a discounted security that you purchased on March 4, 2000, that will mature on May 31, 2011, is discounted at 56.1762, and will be redeemed at face value, or 100. Further assume that you want to use the European, 30-days-in-a-month, 360-days-in-a-year day count basis. To make this calculation, you use the following formula:
=YIELDDISC(“3/4/2000″,”5/31/2011”,56.1762,100,4)
The function returns 0.069412, which is equivalent to 6.9412%.
YIELDMAT
The YIELDMAT function calculates the yield of a security that will pay its interest upon maturity given the settlement date, maturity date, issue date, coupon rate, price, and basis. It uses the following syntax:
YIELDMAT(settlement,maturity,issue,rate,price,basis)
Suppose, for example, that you want to calculate the yield on a security that you purchased on March 4, 2000, was first issued on March 4, 1999, that will mature on May 31, 2011, pays a coupon of 3.5% semiannually, and is priced at 95.8194. Further assume that you want tousetheEuropean,30-days-in-a-month,360-days-in-a-yeardaycountbasis.Tomakethis calculation, you use the following formula:
=YIELDMAT(“3/4/2000″,”5/31/2011″,”3/4/1999”,.035*2,95.8194,4)
The function returns 0.071698, which is equivalent to 7.1698%.
Using the Treasury Bill Add-In Functions
Excel provides three add-in financial functions for analyzing United States Treasury bills: TBILLEQ, which calculates the bond-equivalent yields; TBILLPRICE, which calculates the price of a Treasury bill; and TBILLYIELD, which calculates the yield on a Treasury bill.
The Treasury bill functions use a set of standard arguments: the settlement date, the maturity date, the discount rate, and the price. The settlement date specifies the date the bill issettled,orpurchased.Thematuritydatespecifiesthedatethebillmatures,orexpires.(You may enter these date arguments either as text strings enclosed in quotation marks or as serial date values.) The discount rate specifies the annual discount rate used to price the bill. The price specifies the price per $100 of face value.
All three functions return an error value if the settlement or maturity date isn’t a valid date, if the discount rate is less than zero, if the settlement date falls after the maturity date, or if the maturity date isn’t within one year of the settlement date.
TBILLEQ
The TBILLEQ function calculates the bond-equivalent yield for a Treasury bill given its settlement date, maturity date, and a discount rate. It uses the following syntax:
TBILLEQ(settlement,maturity,discount)
For example, if you want to calculate the equivalent bond yield on a Treasury bill if the settlement date is April 8, 2001, the maturity date is July 15, 2001, and the discount rate is 3%, you use the following formula:
=TBILLEQ(“4/8/2001″,”7/15/2001”,.03)
The function returns the value .03067, or 3.067%.
TBILLPRICE
The TBILLPRICE function calculates the price per $100 of face value for a Treasury bill given the settlement date, the maturity date, and the discount rate. It uses the following syntax:
TBILLPRICE(settlement,maturity,discount rate)
For example, if you want to calculate the price on a Treasury bill if the settlement date is April 8, 2001, the maturity date is July 15, 2001, and the discount rate is 3%, you use the following formula:
=TBILLPRICE(“4/8/2001″,”7/15/2001”,.03)
The function returns the value 99.1833, which means that you would pay $99.1833 for each $100 of Treasury bill face value.
TBILLYIELD
The TBILLYIELD function calculates the yield delivered by a Treasury bill given the settlement date, maturity date, and price. It uses the following syntax:
TBILLYIELD(settlement,maturity,price)
For example, if you want to calculate the yield on a Treasury bill if the settlement date is April 8, 2001, the maturity date is July 15, 2001, and the price is 99.1833, you use the following formula:
=TBILLYIELD(“4/8/2001″,”7/15/2001”,99.1833)
The function returns the value 0.0302482, which is equivalent to 3.0248%.
Leave a Reply